Χημικός δεσμός

Εργαστηριακή άσκηση 2. (Παράδοση στο elearn) Μελετάμε και παραδίδουμε τις εξής ασκήσεις.

• Δυναμικό Lennard-Jones (εκτός ερωτήματος δ).
• Δυναμικό Morse.

Άσκηση (Δυναμικό Lennard-Jones). Θεωρήστε το δυναμικό Lennard-Jones το οποίο περιγράφει χημικό δεσμό μεταξύ δύο ατόμων, \begin{equation} V(r) = D\left(\frac{R}{r}\right)^{12} - 2 \left(\frac{R}{r}\right)^6. \end{equation} (α) Σχεδιάστε το δυναμικό (επιλέξτε τιμές για τις παραμέτρους) καθώς και την αρμονική του προσέγγιση γύρω από το ελάχιστο. (β) Βρείτε την ζώνη κίνησης $r_1 \leq r \leq r_2$ για κάθε τιμή της ενέργειας. Εξηγήστε τις διαφορετικές περιπτώσεις κίνησης που υπάρχουν. (γ) Υπολογίστε την περίοδο της κίνησης για διάφορες τιμές της ενέργειας για τις οποίες έχουμε περιοδική κίνηση. Σχολιάστε πώς συγκρίνεται η περίοδος που βρήκατε με την περίοδο ταλάντωσης στην αρμονική προσέγγιση. (δ) Δώστε τα παραπάνω αποτελέσματα σε γραφική παράσταση.

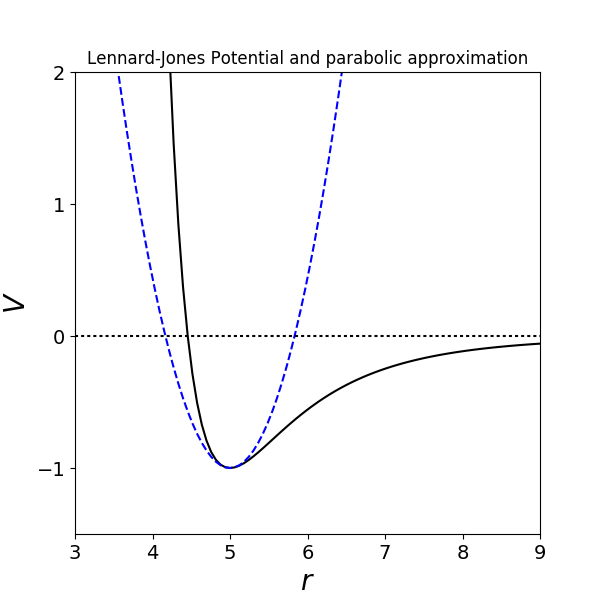
(α) Βρίσκουμε ότι το δυναμικό έχει ελάχιστο στη θέση r₀=R D^1/6 και αυτό έχει την τιμή V(r₀)=-1/D. Η προσέγγιση του V(r) γύρω από το ελάχιστο, σύμφωνα με τον τύπο Taylor, είναι \begin{equation} V(r) \approx V(r_0) + \frac{1}{2}\, \frac{d^2V}{dr^2}\Big|_{r=r_0} (r-r_0)^2. \end{equation} Ορίζουμε την παραβολική προσέγγιση του δυναμικού ως V(r) ≈ V(r₀) + V_h όπου \begin{equation} V_h(\xi) = \frac{1}{2}\, k \xi^2,\qquad \xi = r-r_0,\quad k = \frac{d^2V}{dr^2}\Big|_{r=r_0} = \frac{72}{R^2 D^{4/3}}. \end{equation}

Επιλέγουμε τιμές για τις παραμέτρους R=5, D=1, ώστε έχουμε r₀=5 και V(r₀=5)=-1. Σχεδιάζουμε το V(r) (με μαύρη συνεχή γραμμή) και την παραπάνω αρμονική του προσέγγιση (με μπλε διακεκομμένη γραμμή) με κώδικα python.

(β) Αν έχουμε τιμή ενέργειας E₀ στο διάστημα $-1/D \leq E_0 \lt 0$, το διάστημα κίνησης είναι $r_1 \leq r \leq r_2$ όπου \begin{equation} r_{1,2} = \frac{r_0}{\left( 1 \pm \sqrt{1+D E_0} \right)^{1/6}}. \end{equation}

Για τις τιμές των παραμέτρων $R=5, D=1$ έχουμε \[ r_{1,2} = \frac{5}{\left( 1 \pm \sqrt{1+E_0} \right)^{1/6}}. \]

Έχουμε τις εξής περιπτώσεις:

• Για τιμές ενέργειας $E_0$ με $-1/D \leq E_0 \lt 0$ έχουμε περιορισμένη κίνηση όπως είδαμε στην προηγούμενη παράγραφο.
• Για τιμές ενέργειας $E_0\geq 0$ η κίνηση του σώματος είναι απεριόριστη προς τα δεξιά. Τότε δεν υπάρχει χημικός δεσμός.
• Για τιμές ενέργειας $E_0 \lt -1/D$ οι εξισώσεις κίνησης δεν έχουν λύση.

(γ) Στην περίπτωση που το σύστημα βρίσκεται κοντά στο ελάχιστο της $V(r)$, δηλαδή γύρω από το $r=r_0$, τότε η δυναμική ενέργεια προσεγγίζεται από την $V_h(r)$ και η συχνότητα ταλάντωσης είναι $\omega=\sqrt{k/\mu}$ όπου $\mu$ η (ανηγμένη) μάζα του συστήματος. Θα πάρουμε τιμές για τις παραμέτρους $R=5, D=1, \mu=2$, ώστε έχουμε $k=72/25=2.88$ και η γωνιακή συχνότητα ταλάντωσης στην αρμονική προσέγγιση είναι $\omega=\sqrt{1.44}=1.2$. Η περίοδος είναι $T_h = 2\pi/\omega = 5.24$. Αυτή η προσέγγιση ισχύει για μικρές αποκλίσεις από το ελάχιστο, δηλαδή για $|\xi| \ll 1$.

Ο χρόνος που χρειάζεται το σώμα για να κινηθεί, μέσα σε δυναμικό V(r), από το r₁ στο r₂ δίνεται από το ολοκλήρωμα \begin{equation} \label{eq:1Dpotential_time} \frac{T}{2} = \int_{r_1}^{r_2} \frac{dr'}{\sqrt{\frac{2}{\mu}\,[E_0 - V(r')]}}. \end{equation} Η περίοδος ταλάντωσης είναι $T$ (το διπλάσιο του παραπάνω ολοκληρώματος) αφού μία περίοδος της κίνησης προκύπτει από την κίνηση από το r₁ στο r₂ και πάλι στο r₁.

Δείτε τον κώδικα python ο οποίος (i) υπολογίζει τις ποσότητες που συζητήθηκαν παραπάνω για δεδομένες τιμές των παραμέτρων και (ii) βρίσκει αριθμητικά την περίοδο ταλάντωσης για δεδομένη τιμή της ενέργειας $E_0$.

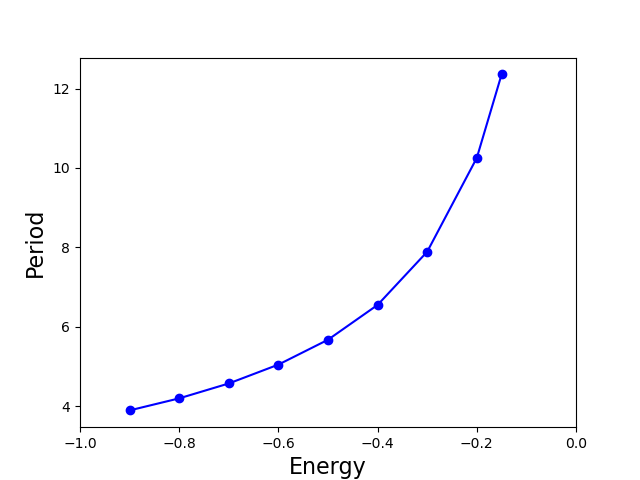
Παρατηρούμε ότι η περίοδος που βρίσκουμε είναι μεγαλύτερη της περιόδου στην αρμονική προσέγγιση για κάθε τιμή της $E_0$.

(δ) Δείτε τον κώδικα python ο οποίος υπολογίζει την περίοδο ταλάντωσης για μία σειρά τιμών της ενέργειας και κάνει γραφική παράσταση της περιόδου $T$ ως συνάρτηση της ενέργειας $E_0$.

Παρατηρούμε ότι $T\to T_h$ για $E_0\to -1/D$. Επίσης $T \gt T_h$ για κάθε τιμή της ενέργειας $0 > E > -1/D$.

Ερωτήσεις

• Με ποιον τρόπο (αλλάζοντας ποιες παραμέτρους) μπορεί να γίνει ο δεσμός μεταξύ των ατόμων ισχυρότερος;
• Τι συμβαίνει στην ειδική περίπτωση $E_0=-1/D$;
• Τι συμβαίνει στην ειδική περίπτωση $E_0=0$;

Μαθησιακά αποτελέσματα

• Μοντελοποίηση χημικών δυνάμεων.
• Κίνηση γύρω από ελάχιστο δυναμικού.
• Χρήση προσεγγίσεως.

Άσκηση (Δυναμικό Morse). Το δυναμικό Morse περιγράφει την αλληλεπίδραση ατόμων σε ένα διατομικό μόριο και έχει την μορφή \[ V(r) = D_e \left( 1 - e^{-(r-r_e)}\right)^2. \] όπου $D_e, r_e$ είναι θετικές σταθερές. (α) Σχεδιάστε το δυναμικό. (β) Βρείτε την απόσταση ισορροπίας $r_0$ των ατόμων. Σχολιάστε τις τιμές του δυναμικού στα $r=0, r_0, \infty$. (γ) Κάνετε την αρμονική προσέγγιση και σχεδιάστε την. (δ) Βρείτε την συχνότητα (ή περίοδο) αρμονικών ταλάντωσεων γύρω από την θέση ισορροπίας. (ε) Δείξτε ότι μία άλλη μορφή του δυναμικού Morse είναι η \[ V(r) = D_e \left( e^{-2(r-r_e)} - 2e^{-(r-r_e)} \right). \]

(α) Χρησιμοποιούμε κώδικα παρόμοιο με τον αντίστοιχο στο Lennard-Jones.

(β) Η απόσταση ισορροπίας $r_0$ βρίσκεται στο ελάχιστο του δυναμικού, \[ \frac{dV}{dr}(r=r_0) = 0 \Rightarrow \ldots \Rightarrow r_0 = r_e. \] Η τιμή του δυναμικού στο ελάχιστο είναι $V(r=r_0)=0$. Επίσης $V(0)=D_e \left( 1 - e^{r_e}\right)^2 > 0$ και $V(\infty)=D_e$.

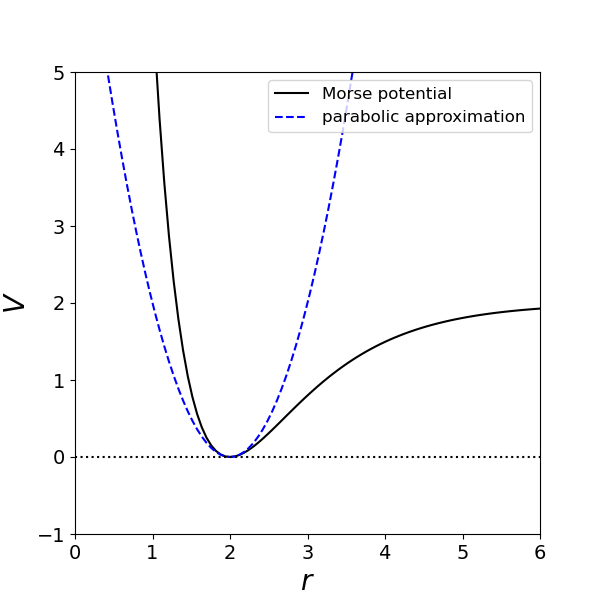
(δ) Το δυναμικό γύρω από την θέση $r=r_0$ προσεγγίζεται από \[ V(\xi) = D_e \xi^2,\qquad \xi = r-r_e. \] Η γωνιακή συχνότητα της περιοδικής κίνησης είναι $\omega=\sqrt{2D_e/m}$, όπου m η μάζα του συστήματος.

(ε) Το τετράγωνο δίνει τρεις όρους. Μπορούμε να παραλείψουμε τον σταθερό όρο διότι δυναμικά που διαφέρουν κατά σταθερά είναι ισοδύναμα. Η νέα μορφή του δυναμικού έχει τιμή στο ελάχιστο $V(r=r_0)=-D_e$.

Άσκηση (Δυναμικό με ελάχιστο). Σώμα μάζας $m$ κινείται στον άξονα $x$ σε δυναμική ενέργεια \[ V (x) = −Ax e^{−αx}, \] όπου $A, a$ είναι θετικές σταθερές. (α) Βρείτε τη θέση ισορροπίας της μάζας. (β) Κάνετε την αρμονική προσέγγιση για κινήσεις κοντά στη θέση ισορροπίας και βρείτε την περίοδο αρμονικών ταλάντωσεων γύρω από αυτήν. [Υπόδειξη. Επιλέξτε συγκεκριμένες τιμές για τα $A, a$.]

Άσκηση (Περιοδική κίνηση σε δυναμικό). Επιλέξτε ένα δυναμικό $V(x)$ το οποίο έχει ένα τουλάχιστον ελάχιστο. Βρείτε την ζώνη κίνησης $x_1 \leq x \leq x_2$ για δεδομένη τιμή της ενέργειας $E=E_0$. Υπολογίστε την περίοδο της κίνησης για μία σειρά τιμών της ενέργειας. Δώστε τα παραπάνω αποτελέσματα σε γραφική παράσταση.

Δείτε κώδικα python ο οποίος βρίσκει την ζώνη κίνησης και υπολογίζει την περίοδο ταλάντωσης για μία σειρά τιμών της ενέργειας. Επίσης, κάνει γραφική παράσταση της περιόδου T ως συνάρτηση της ενέργειας E₀.