Δυναμική πληθυσμών

Εργαστηριακή άσκηση 4. (Παράδοση στο elearn) Μελετάμε και παραδίδουμε όλες τις παρακάτω ασκήσεις.
Παραδίδουμε ένα αρχείο στο οποίο δίνονται οι απαντήσεις των θεωρητικών ερωτημάτων και επίσης περιέχονται τα σχήματα (σχεδιασμένα από υπολογιστή) όπου χρειάζονται. (Μπορείτε να οργανώσετε και διαφορετικά την υποβολή σας αν προτιμάτε, αλλά φροντίστε να ακολουθείται μία λογική σειρά ώστε να μπορεί κανείς να παρακολουθήσει τις λύσεις.) Οι "Ερωτήσεις" (στο τέλος κάθε άσκησης) είναι για την εξάσκησή σας και μόνο (δεν τις παραδίδουμε).

Άσκηση (Αδιαστατοποίηση Λογιστικού μοντέλου). Το λογιστικό μοντέλο περιγράφει την εξέλιξη ενός πληθυσμού N ο οποίος αναπτύσσεται με μέγιστο ρυθμό r σε ένα οικοσύστημα περιορισμένης χωρητικότητας K, \[ \frac{dN}{dt} = r N \left(1- \frac{N}{K} \right). \] (α) Κάνετε αδιαστατοποίηση του μοντέλου. (β) Επίσης γράψτε την αδιάστατη μορφή της λύσης του (την οποία μπορείτε να βρείτε στις σημειώσεις).

(α) Ορίζουμε κανονικές μεταβλητές \[ n := \frac{N}{K},\qquad \tau := r t, \] αντικαθιστούμε στην αρχική εξίσωση και έχουμε \[ \frac{d n}{d\tau} = n (1-n) \] την κανονική μορφή της εξίσωσης.

(β) Αν θεωρήσουμε αρχική συνθήκη N(t=0) = N₀, η λύση του προβλήματος αρχικών τιμών (για την αρχική εξίσωση) είναι \[ N(t) = \frac{N_0 Ke^{rt}}{K+N_0 (e^{rt}-1)}. \] Χρησιμοποιούμε τις αδιάστατες μεταβλητές στην λύση και έχουμε \[ n(\tau) = \frac{n_0\,e^\tau}{1+n_0 (e^\tau-1)}. \] όπου έχουμε ορίσει n₀=N/N₀.

Ερωτήσεις

• Μπορείτε να εξαγάγετε την γενική λύση του αδιάστατου μοντέλου;

Μαθησιακά αποτελέσματα

• Αδιαστατοποίηση μοντέλων.

Άσκηση (Λογιστικό μοντέλο με συγκομιδή). Εάν περιλάβουμε συγκομιδή με ρυθμό ανά μονάδα πληθυσμού $E$, το λογιστικό μοντέλο γίνεται \[ \frac{dN}{dt}=rN\left( 1- \frac{N}{K} \right)-EN. \] (α) Βρείτε τα σημεία ισορροπίας του μοντέλου και περιγράψτε τις περιοχές παραμέτρων για τις οποίες έχουμε τα σημεία ισορροπίας που βρήκαμε. (β) Γραμμικοποιήστε το μοντέλο γύρω από κάθε σημείο ισορροπίας.

Δείτε στο σύγγραμμα το Κεφ. 5.2.3. Παρακάτω θα δοθούν συνοπτικές απαντήσεις.

(α) Τα σημεία ισορροπίας είναι \[ N_0 = 0\qquad N_h = K\left(1-\frac{E}{r}\right). \] Το σημείο N=N_h υπάρχει μόνο όταν E < r.

(β) Θέτουμε F(N) = N(r-E-rN/K) και υπολογίζουμε \[ F'(N_0) = r-E\qquad F'(N_h) = E-r. \] Για το N=N_h έχουμε την γραμμικοποιημένη εξίσωση \[ \frac{d\epsilon}{dt} = (E-r) \epsilon,\qquad \epsilon = N-N_h \] ώστε αυτό είναι ένα ευσταθές σημείο ισορροπίας για E < r. Μπορούμε να κάνουμε παρόμοια ανάλυση και για το N=0.

Ερωτήσεις

• Σε ποια κατάσταση καταλήγει το σύστημα για μεγάλους χρόνους; (δηλαδή ποιο είναι το όριο $N(t\to\infty)$;)

Μαθησιακά αποτελέσματα

• Γραμμικοποίηση εξισώσεων.

Άσκηση (Μοντέλο Lotka-Volterra). Μελετήστε το μοντέλο Lotka-Volterra για τους πληθυσμούς δύο ειδών N (θηράματος) και P (κυνηγού) \[ \dot{N} = a N - c N P \qquad \dot{P} = -b P + d N P. \] (α) Βρείτε τα σημεία ισορροπίας του συστήματος (κάνετε μία δική σας επιλογή για τις παραμέτρους a, b, c, d > 0).
(β) Βρείτε μία αριθμητική λύση (για αρχική συνθήκη της επιλογής σας) και σχεδιάστε τους πληθυσμούς ως συναρτήσεις του χρόνου N=N(t), P=P(t).
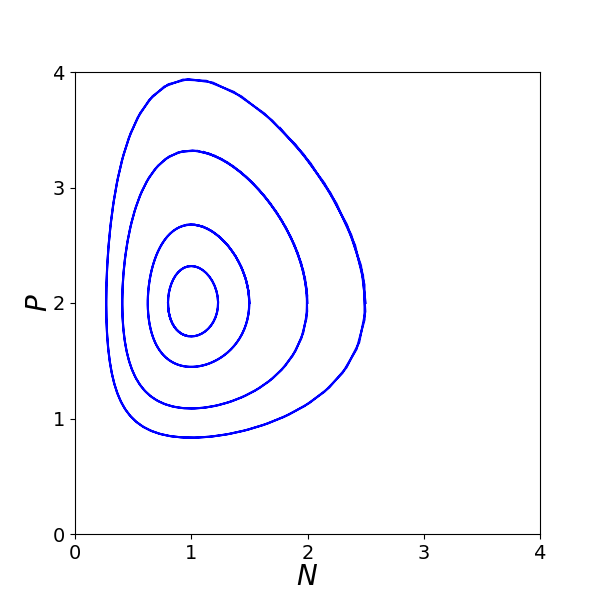
(γ) Βρείτε περισσότερες αριθμητικές λύσεις και σχεδιάστε αρκετές καμπύλες στον χώρο των φάσεων (N, P).
(δ) Σχεδιάστε τις καμπύλες στο χώρο των φάσεων χρησιμοποιώντας το ολοκλήρωμα του συστήματος εξισώσεων.

(α) Ας επιλέξουμε τις σταθερές a=2, b=1, c=1, d=1. Τα σημεία ισορροπίας είναι τα (N,P)=(0,0) και (N,P)=(b/d,a/c)=(1,2).

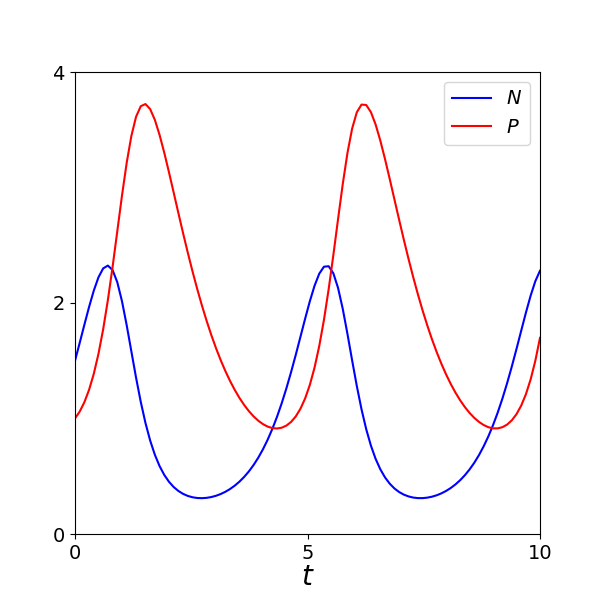
(β) Δείτε στο σχήμα το αποτέλεσμα του κώδικα.

(γ) Δείτε στο σχήμα το αποτέλεσμα του κώδικα.

(δ) Το ολοκλήρωμα είναι \[ (cP − a \ln P) + (dN − b \ln N) = C \] Σχεδιάζουμε ισοσταθμικές καμπύλες με τον κώδικα.

Ερωτήσεις

• Σε ποιες καμπύλες στο διάγραμμα φάσεων αντιστοιχούν οι λύσεις που σχεδιάσαμε στο ερώτημα (β);
• Σχεδιάστε επάνω σε μία καμπύλη του διαγράμματος φάσεων διαδοχικά σημεία τα οποία ισαπέχουν στο χρόνο. Σε ποιες περιοχές είναι ταχύτερη η μεταβολή των μεταβλητών (x,y) και σε ποιες βραδύτερη;

Μαθησιακά αποτελέσματα

• Λύση συστήματος δύο διαφορικών εξισώσεων.
• Χρονική εξέλιξη συστήματος δύο πληθυσμών.
• Γραφική αναπαράσταση λύσεων στον χώρο φάσεων.

Άσκηση (Μοντέλο επιδημιών). Θεωρούμε το μοντέλο επιδημιών SIR, \[ \dot{S} = -\beta SI \qquad \dot{I} = \beta SI - \gamma I \qquad \dot{R} = -\gamma I. \] (α) Λύστε αριθμητικά το πρόβλημα (επιλέξτε παραμέτρους και αρχικές συνθήκες της προτίμησής σας). (β) Επαληθεύστε ορισμένα από τα αναλυτικά αποτελέσματα τα οποία είναι γνωστά για το σύστημα, (i) την θέση του μεγίστου της επιδημίας, (ii) τον αριθμό μολυσμένων στο μέγιστο και (iii) τον ολικό αριθμό μολυσμένων κατά την πλήρη διάρκεια της επιδημίας. [Υπόδειξη. Θα χρειαστεί να παρουσιάσετε σχήμα από τον υπολογιστή για να απαντήσετε σε αυτή την ερώτηση.]

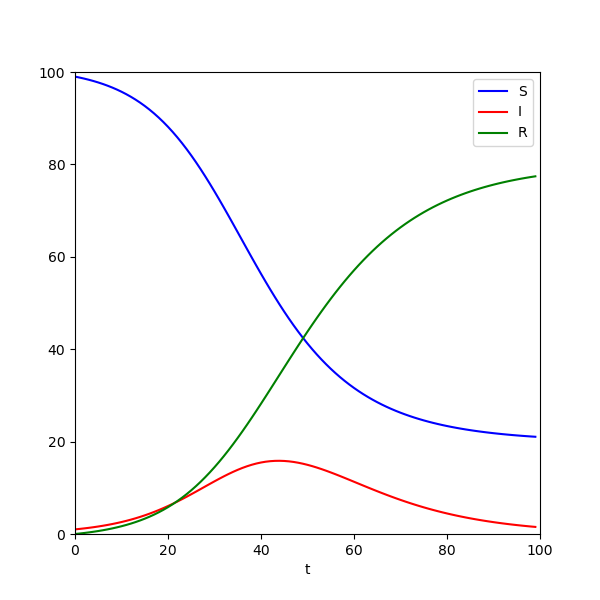
(α) Δείτε στο σχήμα το αποτέλεσμα του κώδικα κώδικα.

(β) Ας επιλέξουμε $N=100,\, \beta=0.002,\, \gamma=0.1$.

Το μέγιστο της επιδημίας συμβαίνει για $S=\gamma/\beta=50$. Την στιγμή εκείνη ο αριθμός μολυσμένων είναι \[ I_m = (N-S_m) - S_m\ln(N/S_m) \approx 15.3,\qquad S_m=\gamma/\beta. \] Στο σχήμα βλέπουμε ότι το μέγιστο της επιδημίας συμβαίνει για χρόνο $t\approx 45$ και εκεί έχουμε $S=50, I=15.3$ (χρειάζεται να δούμε τα νούμερα που βγάζει ο κώδικας για να το επιβεβαιώσουμε αυτό με ακρίβεια, είτε να κάνουμε ένα πιο λεπτομερές σχήμα).

O αριθμός αυτών που δεν μολύνθηκαν κατά την πλήρη διάρκεια της επιδημίας δίνεται ως λύση της \[ (N-S_0) - S_m \ln (N/S_0) = 0. \] Ο ολικός αριθμός οι οποίοι έχουν μολυνθεί κατά την πλήρη διάρκεια της επιδημίας είναι \[ I_0 = N - S_0. \]

Ερωτήσεις

• Για ποιες τιμές των $\beta, \gamma$ έχουμε επιδημία;
• Αλλάξτε την τιμή του β στον κώδικα ώστε η επιδημία να κρατήσει λιγότερο χρόνο.
• Αλλάξτε την τιμή του β στον κώδικα ώστε το μέγιστο του $I$ να γίνει μικρότερο.
• Σε ποιές καμπύλες στο διάγραμμα φάσεων του ερωτήματος (γ) αντιστοιχούν οι λύσεις που σχεδιάσαμε στο ερώτημα (β);
• Σχεδιάστε επάνω σε μία καμπύλη του διαγράμματος φάσεων διαδοχικά σημεία τα οποία ισαπέχουν στο χρόνο. Σε ποιες περιοχές είναι ταχύτερη.

Μαθησιακά αποτελέσματα

• Σύγκριση αναλυτικών και αριθμητικών αποτελεσμάτων.

Άσκηση (Μοντέλο για οπαδούς παράταξης). Έστω ότι σε ένα πανεπιστήμιο δραστηριοποιείται η φοιτητική παράταξη Α. Ένα ποσοστό (έστω r) των οπαδών της δραστηριοποιείται έντονα και πείθουν ο καθένας ένα νέο φοιτητή κάθε χρόνο να ενταχθεί στην παράταξη. Επίσης λαμβάνουμε υπόψιν ότι ένα ποσοστό (έστω s) των οπαδών αποφοιτά κάθε χρόνο. (α) Γράψτε ένα μοντέλο για τον αριθμό των οπαδών της παράταξης σαν συνάρτηση του χρόνου.
Ακολούθως, θεωρούμε ότι από τον συνολικό αριθμό των φοιτητών του πανεπιστημίου Φ μόνο ένα ποσοστό (έστω p) είναι δυνατόν να πεισθεί από την παράταξη Α ενώ οι υπόλοιποι είναι εξαιρετικά δύσκολο να γίνουν οπαδοί της (για ιδεολογικούς και άλλους λόγους). (β) Γράψτε ένα νέο μοντέλο για τον αριθμό των οπαδών της παράταξης εισάγοντας τη λογιστική ανάπτυξη (logistic growth) ώστε να λάβετε υπόψιν την παραπάνω παρατήρηση (θεωρήστε r > s). (γ) Ορίστε αδιάστατες (κανονικές) μεταβλητές και γράψτε την κανονική μορφή της εξίσωσης (του (β) ) στις νέες μεταβλητές.

(α) Έστω N ο αριθμός των φοιτητών της παράταξης Α. Έχουμε αύξηση του N ανά έτος (λόγω νέων οπαδών) κατά rN και μείωση (λόγω αποφοίτησης) κατά sN. Ώστε ο ρυθμός μεταβολής του N είναι \[ \frac{dN}{dt} = (r-s) N. \]

(β) Θέτουμε α := r-s και έχουμε r > s $\Rightarrow$ α > 0. Σε αυτή την περίπτωση το μοντέλο (α) θα έδινε $N(t) \to \infty$ για $t \to \infty$. Αν εισάγουμε τη λογιστική ανάπτυξη έχουμε το μοντέλο \[ \frac{dN}{dt} = \alpha N \left( 1 - \frac{N}{K} \right) \] όπου K := pΦ. Βλέπουμε ότι $N(t) \to K$ για $t \to \infty$.

(γ) Ορίζουμε κανονικές μεταβλητές \[ n := \frac{N}{K},\qquad \tau := \alpha t \] αντικαθιστούμε στην εξίσωση του (β) και έχουμε \[ \frac{d n}{d\tau} = n (1-n) \] την κανονική μορφή της εξίσωσης.

Ερωτήσεις

Μαθησιακά αποτελέσματα

• Κατασκευή λογιστικού μοντέλου.