Μάθημα 1 : Σταθερές

> 4+5;

> 4+5 ?help # πρέπει να μπαινει ';' στο τέλος

Syntax error, character `?` unexpected

> 4+2*5;

> 100*365*24*60; # πόσα λεπτά ζωής σε 100 χρονια (περίπου)

> (")*60; #πόσα δευτερόλεπτα ζωής σε 100 χρόνια περίπου

> pi;

> Pi;

> evalf(");

Σημείωσε ότι το Pi ειναι διαφορετικό από το pi.

> Digits ;

> Digits := 30;

> evalf(Pi);

> evalf(Pi, 100);

Κατάλογος με όλες τις σταθερές που διαθέτει το πρόγραμμα:

> constants;

> 3/7 + 5/11;

> evalf(");

> 2^8;

> 2^16;

> 2^32;

> 2^64;

To δυαδικό σύστημα παράστασης αριθμών. Τα α0, ...., α7 ειναι τα 8 ψηφία (παίρνουν τις τιμές 0 ή 1) ενος αριθμού γραμμενου στο δυαδικό σύστημα

> a7*2^7+a6*2^6+a5*2^5+a4*2^4+a3*2^3+a2*2^2+a1*2^1+a0*2^0;

> convert( 7, binary ); # 111 = 1*4 + 1*2 + 1*1

> convert( 111011001, decimal, binary ); # η αντίστροφη διαδικασία

> convert( 11111111111111111111111111111111, decimal, binary ); # ο πίο μεγάλος 32-ψήφιος στο 2-δικό σύστημα

exp(1);

> evalf(");

> constants := constants, e ;

> e := exp(1); #ορισμός τιμής νέας σταθεράς

> evalf(e);

> 4!;

> 5!

> ;

> 10!

> ;

> 1/10!;

> 1.0/10!;

> Digits := 10;

> 1.0/10!;

Μερικές από τις συναρτήσεις της θεωρίας αριθμών:

> ifactor(50);

> ifactor(13333);

> ifactor(13331); #πρώτος !

> ifactor(12321);

> ifactor(1234321);

> ifactor(123454321);

> ifactor(12345654321);

Το ερώτημα: είναι όλοι αυτοί οι αριθμοί μη-πρώτοι;

> expand(");

> isprime(12345654321);

> igcd(11,121);

> igcd(112, 22232);

> ilcm(2,3,5,7);

> ilcm(4,12,70,14);

Πραγματικοί αριθμοί σε αντίθεση με τους φυσικούς, γράφονται με μιά τελεία για δεκαδικά ψηφία.

> 1./3.;

> 1/3;

> eval(1/3);

> evalf(1/3);

> iquo(23/5); # πραξεις με ακεραίους

Error, wrong number (or type) of parameters in function iquo

> iquo(23,5);

> irem(23,5);

Αθροισμα ρητών μετατρέπεται σε πραγματικό ακόμη και με μία εμφάνιση τελείας:

> 1/2+1/3+1/5+1/7;

> 1/2+1/3.+1/5+1/7;

Ακολουθίες ρητών αριθμών:

> seq( i/(i+1), i=1..10);

> seq( (i+1)/i, i=1..12);

> seq( i^2/(i+1)^3, i=1 .. 10 );

> sum( 1/i, i=1..10);

> Sum( 1/i, i=1..10);

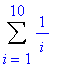
> sum(i, i=1..20);

> sum(i^2, i=1..10);

Τυχαίος ακεέραιος αριθμός με 12 ψηφία:

> rand();

> rand();

> rand();

> length(%); #πόσα ψηφία ...

Και λίγα για μιγαδικούς. Ι παριστάνει την φανταστική μονάδα

> 3+4*I;

> (1+I)/(1-2*I); # διαίρεση μιγαδικών

> cos(Pi/4)+I*sin(Pi/4);

> eval(%);

Εύρεση μεγίστου ελαχίστου:

> max(2^3/4!, 3^2/3!);

Συνδυασμοί n ανά k:

> binomial( 5,3);

> expand( (a+b)^5 );

> expand( (a+b)^10 );

Από την γραμμική άλγεβρα:

> vector(3, [a,b,c]);

> vector(4, [1,2,3,4]);

> vector(7, [a, b, 1,2,3,4,c]);

> vector(2, [1,3]) + vector(2, [2,5]);

Πρώτα φορτώνουμε το πακέτο Γραμμικής Άλγεβρας.

> with linalg;

Syntax error, missing operator or `;`

> with (linalg):

Warning, new definition for norm

Warning, new definition for trace

Εισάγουμε μερικά τυχαία διανύσματα. (Η εντολή randvector(n) δημιουργεί ένα διάνυσμα διάστασης n με τυχούσες συντεταγμένες.)

> randvector(3);

> randvector(10);

> randmatrix(3,3);

> det(");

> randmatrix(3,3);

> inverse(");

> matrix(3,3,[1,2,3,4,5,6,7,8,9]);

> matadd(",");

> det(");

> matrix(3,1,[1,2,3]);

> randmatrix(3,2);

> transpose(");

> inverse(");

Error, (in inverse) expecting a square matrix

Ορισμός πίνακα με τύπο:

> matrix(4,5,(i,j)->1/(i+j));

> matrix(5,5, (i,j)->if i<>j then 1/(i*j) else 1 fi );

> col(",3);

> stack( vector(3,[1,2,3]), vector(3, [7,7,7]) ;

Syntax error, `;` unexpected

> stack( vector(3,[1,2,3]), vector(3, [7,7,7])) ;

> row(",2);