Μάθημα 2 : Μεταβλητές

> x = 4; #δεν γινεται αυτό που περιμένω

> eval(x);

> evalf(x);

> x:=7; # τώρα μάλιστα

> x;

> 2*x;

> x^2;

> x = x+10; # ασυναρτισίες

> x:=x+10; # τώρα μάλιστα

> y := x^2;

> evalf(x+y);

> w := x + y;

> x; y; w;

Eάν αλλάξω την τιμή του x, πρέπει να τρέξω και τις εντολές που ορίζουν τα y, w, γιά να έχω τις αντίστοιχες τιμές

> N:=5;

> c := (a+b)**N;

> expand(c);

> a=1; b=1; c;

> a:=1; b:=1;c;

> expand(c);

Ανάλογα με τις πράξεις που έχουν προηγηθεί, η μεταβλητή θεωρήται συμβολική ή συγκεκριμένη σταθερά.

> (3*x+5*y)+ (4*x+10*y); # δεν κάνει συμβολική πρόσθεση αλλά αριθμητική

> restart; a := (3*x+5*y); b:= (4*x+10*y);

H restart καθαρίζει την μνήμη και έτσι τα x, y γίνονται συμβολικές μεταβλητές και οι πράξεις γίνονται κι' αυτές συμβολικά.

> c := a*b; expand(c );

> d:=c*(a+b);

> expand(d);

> d;

> d:=expand(d);

> factor(d);

> e:= d+(a*x+5)*(b*x+2);

> factor(e);

Αυτά για μεταβλητές που παριστούν ακεραίους, πραγματικούς αριθμούς . Πάμε τώρα στα διανύσματα. Μεταβλητές που παριστούν ένα όλόκληρο διάνυσμα.

> restart; with(linalg):

Warning, the protected names norm and trace have been redefined and unprotected

> a:=[1, 2, 3, 4, a];

Error, recursive assignment

> a:=[1, 2, 3, 4, b];

> b:=10; a;

> b:=[2,2,2];

> b;a;

> b:= 100; a;

> a:=[1,2,3,4,5]; b:=[11,12,13,14,15];

> a+b; # πρόσθεση διανυσμάτων

> c:= randmatrix(3,3); d:= randmatrix(3,3);

> c+d; #δεν δουλεύει η πρόσθεση για πίνακες

> evalm(%); #αυτό δουλεύει για πίνακες

> evalm(%+transpose(%));

Mεταβλητές είναι χρήσιμες όταν θέλουμε να κάνουμε διάφορες πράξεις με το ίδιο αντικείμενο.

> restart; with(linalg): a := randmatrix(3,3);

Warning, the protected names norm and trace have been redefined and unprotected

> b:=a+transpose(a);

> evalm(b);

> evalm(b*b);

> c:=inverse(b);

> d:=matrix(3,1, [10,20,30]);

> e:= evalm(c*d);

Error, (in evalm/evaluate) use the &* operator for matrix/vector multiplication

> e:= evalm(c&*d);

> v1:= vector(3,[4,5,6]); v2:= vector(3, [7,8,9]);

vvv:= innerprod(v1,v2);

> www := crossprod(v1,v2);

> innerprod(www,v1); innerprod(www,v2);

> norm(v1); norm(v2); norm(v1+v2); # Δεν είναι η γνωστή (αυτή βρίσκει την απολύτως μέγιστη συνιστώσα)

> norm(v1,2); norm(v2,2); norm(v1+v2,2);

> det(b);

Για πολυώνυμα υπάρχουν ανάλογες χρήσεις των μεταβλητών

> restart; p:= (x+y)^2;

> op(p);

> expand(p);

> q := p*p; expand(q);

> x:=1; y:=2; p;

> expand(p); # εχει πλέον αριθμητική σημασία και όχι συμβολική όπως πρίν

> restart; solve(3*x = 4, x);

> solve( a*x^2+b*x+c =0, x ); # τριώνυμο

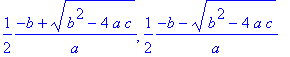
> solve( {a*x+b*y=e, c*x+d*y=f}, {x,y} ); # τομή δύο ευθειών

> Equations := {x^2+y^2+a*x+b*y+c=0, e*x+f*y+g=0}; Variables := {x,y};

> solve(Equations, Variables ); #τομή κύκλου και ευθείας

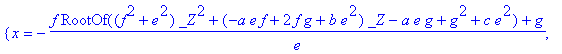
> allvalues(%);

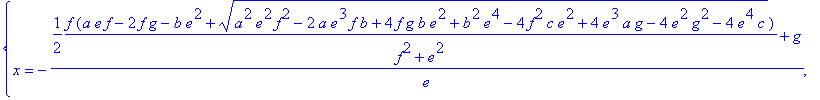
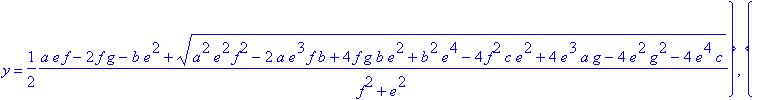
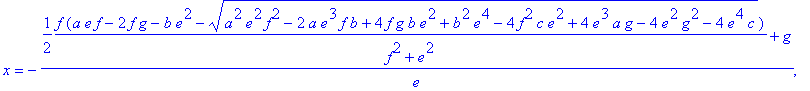
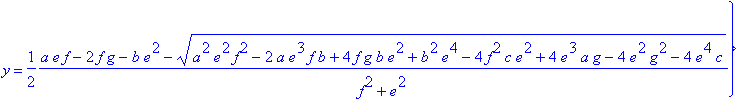
> a:=1; b:=5; c:=1; e:=1; f:=1; g:=1; solve(Equations, Variables);

> allvalues(%);

>