Μάθημα 3 : Συναρτήσεις

> x := 3;

> cos(x); tan(x);

> evalf(%);

> y := { cos(x), sin(x), abs(1-x), ln(x), sqrt(x), tan(x), sinh(x), exp(x), power(x,5)};

> evalf(y);

Αυτές είναι οι προκαθορισμένες, γνωστές συναρτήσεις. Μπορεί κανείς να ορίσει δικές του:

> f := x->x^2; g:= x-> 1/(1+x^2);

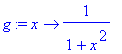
> plot([f, g], -2..2, color=[black,blue], style=[line,line], thickness = [2,4]);

> myEqua := {f(z)-g(z)=0};

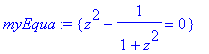
> solve( myEqua,{x} );

Error, (in solve) a constant is invalid as a variable, 3

> mySolutions := solve( myEqua,{z} ); # δεν αναγνώριζε το x σαν μεταβλητή

> mySolutions[3];

> type(%,realcons); # δεν είναι πραγματική

> subs( mySolutions[1] , myEqua ); # επαλήθευση της εξίσωσης από την πρώτη λύση που βρήκε

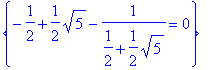
Δύο ακόμη συναρτήσεις.

> ff:=w->(w^2+3*w)/(w^4+w+1);

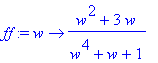
> plot(ff,-infinity..infinity);

> plot( arctan, -infinity..infinity ); #από τις συναρτήσεις που έχει έτοιμες η Maple

> # ?inifcns; # βγάλτε το πρώτο # και εκτελέστε για να δείτε τις έτοιμες προς χρήση συναρτήσεις

Eξετάζω την σύνθεση συναρτήσεων φ(φ(φ...φ(x))...).

> myfun:= x->cos(x); myfun5:= myfun@@5;

> myfun(Pi); myfun5(Pi);

> myBigFun := (N,x)->(myfun@@N)(x);

Η επόμενη ακολουθία αριθμών είναι η {xN = cos(cos(....cos(0)...)) (N φορές) }. Τι παρατηρείς?

> seq( evalf(myBigFun(N,0)) , N=1..65 ); # αντικατάστησε το 0 με οτιδήποτε, αύξησε το Ν

> myId:= x->x; myFun:= x->cos(x);

> plot([myId, myFun], -3..3, color=[green,blue], style=[line,line], thickness = [2,4]);

>

> solve( myId(x)-myFun(x)=0, x );

Error, (in solve) a constant is invalid as a variable, 3

> solve( (myId-myFun)(x)=0, x );

Error, (in solve) a constant is invalid as a variable, 3

> allvalues(%);

Τι συμπέρασμα βγαίνει απ' αυτό και τα προηγούμενα? Τι παριστάνει το μυστήριο 0.7390851332 ; Πως να πάρω ενδείξεις αν είναι ρητός ή άρρητος;

Συναρτήσεις που ορίζονται από πολυώνυμα:

> restart;

> myPol:= x-> x^4-6*x^3-2*x^2-x-5; # πολυωνιμική συνάρτηση

> ekfrasi := x^4-6*x^3-2*x^2-x-5; # πολυωνιμική παράσταση

> plot(ekfrasi, -4..7); # δεν αναγνωρίζει σαν συνάρτηση

Plotting error, empty plot

> plot(myPol, -4..7);

Σε αντίθεση με τις συναρτήσεις, πολυωνυμικές εκφράσεις μπορούμε να τις διερευνήσουμε ως προς τον βαθμό, συντελεστές κτλ.

> deg:= degree(ekfrasi,x);

> coeffs(ekfrasi,x); # δίνει τους συντελεστές αλλά χωρίς διάταξη

> seq( coeff( ekfrasi, x, i ), i=0..deg ); # κατ' αύξουσα διάταξη

> solve(ekfrasi, x);

> solve( myPol(x)=0, x );

> fsolve(ekfrasi, x); fsolve( myPol(x)=0, x ); # πραγματικές (αριθμητικές) ρίζες

> fsolve(ekfrasi, x, complex ); # όλες οι ρίζες πραγματικές + μιγαδικές

Στις εκφράσεις γίνονται αντικαταστάσεις μεταβλητής, τυπικές και αριθμητικές

> subs(x=t,ekfrasi);

> subs(x=1, ekfrasi);

> subs( x=1, myPol ); #όμως σε συναρτήσεις

> subs( x=t, myPol );

> ekfr2:= x*(x-2)+m; #ομως αν σε συνάρτηση υπάρχει παράμετρος, γίνεται αντικατάσταση

> fun2:= x->ekfr2(x);

> m:=-1;

> ekfr2;

> fun2;

> plot(fun2(x), x=-2..2); # ομως αποτυγχάνει η ...

> plot(fun2, -2..2); #δεν γίνεται όταν η συνάρτηση ορίζεται μέσω έκφρασης

Plotting error, empty plot

Χρειάζεται λοιπόν διάκριση του πότε έχω μιά συνάρτηση και πότε μιά αλγεβρική παράσταση (έκφραση) με κάποιες σταθερές και κάποιες μεταβλητές.

> expand(ekfrasi^2);

> degree(%);

> expand(myPol^2);

> degree(%);

> eval(ekfrasi(t));

> eval(myPol(t));

> evalf(ekfrasi(1));

> evalf(myPol(1));

Μετατροπή μιάς έκφρασης σε συνάρτηση:

> polFun:= unapply( ekfrasi, x );

> evalf(polFun(1));

Ο κανόνας λοιπόν είναι να κάνω απλοποιήσεις, πράξεις, παραγοντοποιήσεις αλγεβρικές με εκφράσεις και όταν θέλω την αντίστοιχη συνάρτηση (π.χ. για να κάνω το γράφημα) να εφαρμόζω την "unapply", όπως προηγουμένως, και να ορίζω την αντίστοιχη πολυωνυμική συνάρτηση.

> aa:=3; bb:=-5;

> cladotiSynartisi := x->piecewise( x<=0,-x^2, 0<x and x<=2, aa*x^2+bb*x, 4-x^2/2 );

> plot( cladotiSynartisi, -2..4);

Εντολή που ορίζει μιά κλαδωτή συνάρτηση. Δηλαδή, συνάρτηση που δίνεται από διαφορετικούς τύπους σε διαφορετικά διαστήματα.